| home | library | feedback |
In dependency modeling each model is a set of statements about the the dependencies between sets of variables.
» More about concept of dependency
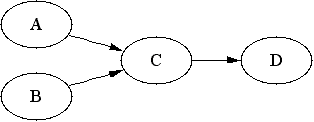
Here is a small example about models. It is not necessary for you to try to study the models in great detail (but you are welcome to do so if you like). The example just tries to give you some idea about the dependency models. So let us assume that our model has four variables A, B, C and D. Following list of statements is a dependency model (we call this model M1):
Such a list looks pretty awkward, but this is what the dependency models are: set of statements about dependencies. Luckily the dependencies above can be also presented in a simple graphical format called Bayesian networks.

We will not yet explain why the picture above is a representation of M1. For now it is enough to know that M1 has this nice representation as a Bayesian network. But before we are lead to think dependency models as graphs, let us look at another dependency model (and let us call this model M2):
This model can also presented as a Bayesian network. The bad news is that there are three different Bayesian networks, that all describe M2 graphically.
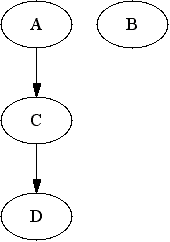 |
 |
 |
| First version | Second version | Third version |
You may notice that the Bayesian networks above are not totally different. Actually, if you strip away the arrowheads, they are all similar. The dependency model M1, however, has only one Bayesian network that represents it. So for some dependency models (like for M1) there is only one Bayesian network that presents it, but for some (like M2) there are many (slightly different) Bayesian network representations. Somewhat more confusingly let us take a look at yet another dependency model (let's call it M3):
Dependency model M3 cannot be represented as a Bayesian network, that is, there does not exist a Bayesian network that represents M3. All this detail can be confusing, so here is the summary of the important points to remember about the models and their Bayesian network presentations.
We still have not yet defined what are these Bayesian networks anyway (is any picture of circles and arrows a Bayesian network?) And how do these Bayesian networks represent the dependencies, i.e., how does one read dependencies from the Bayesian networks? That all will be explained, but before that we have an important announcement to make:
B-Course will only try to build dependency models that can be represented by at least one Bayesian network.
This is not a small restriction, on the contrary, it will leave many interesting dependency sets out of consideration. The reason for this limitation is mainly technical not fundamental. It is easier to search for the model if we make this restriction.
» More about size of model space
» More about models left out
Bayesian network consists of nodes and arcs that can connect pairs of nodes. There is exactly one node for each variable. There is still an extra restriction that arcs are not allowed to form loops. That means that if you can follow the arcs so that you visit some node twice, the thing is not a Bayesian network. Below you can find an example of the network that is not a Bayesian network.
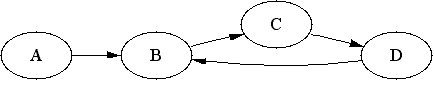
This is generally a rather difficult issue to explain. We will tackle it anyway. The easiest way is to think it as a game. Let us think that we have a Bayesian network with at least two variables A and B (you should think that there is at least three) and let us think that we have a (possibly empty) set S that can contain some other variables of the network (that is any other than A or B). Now your task is to find out whether A and B are dependent given S (that is a short way of saying that A and B are dependent on each other if you know something about all the variables in S and you do not know nothing about those variables that are not in S). So how can you find that out?
This is the answer: A and B are dependent given S if you can freely travel the arcs from A to B. If you cannot freely travel the arcs from A to B, A and B are not dependent given S. Notice that we did not say "follow" the arcs, we said "travel" the arcs. Traveling the arcs is different from following, since when traveling the arcs you can usually go across the arc without caring about the direction of the arc. If S is empty you can travel the arcs forward and backward as long as you never visit the same node twice and your route does not have a situation where you first travel the arc forward and immediately after that travel some other arc backward (we call these forward-backward combinations "collisions" since the arcs in this route collide. The node at which the arcs collide is called a collision node). Here's where the variables belonging to S step into the game. Your traveling route is blocked if it goes through any non-collision nodes that are members of S. This way S:s can block the route even if the node is not n collision node. But S members are not all bad, since sometimes they can help you go through the collisions. You can go through the collision if the collision node or some of its descendants (or both) belong to S. (By descendants of X we mean all the nodes that can be reached by following(!) the arcs that leave from X).
» References to the material about Bayesian networks
So far we have talked about "variables" without any extra qualifications. All the things said are actually true for general random variables, so we have not taken any liberties. However, B-Course will only build dependency models for categorical (discrete) data. It will accept continuous data too, but it will transform it categorical internally before the analysis.
» Read more about categorization
| B-Course, version 2.0.0 | |