Probability of the dependency model

Bayes rule makes it possible for us to update our belief about the true model after we have seen the data. In Bayesian setting this means calculating the probability of the dependency model. The details are somewhat technical but the general idea is easy to explain.

Bayes rule makes it (almost) possible

Now some mathematics. Let us denote our dependency model with a letter M and our data with letter D. Bayes rule says that we can calculate probability of the dependency model M if we have the data D as follows:

P(M | D) = P(D | M) * P(M) / P(D)

The formula above says that once we have the data D the probability of the model M (P(M|D)) can be calculated by first multiplying the probability that the model gives to the data (P(D|M)) with the probability of the model before we had the data (P(M)), and then dividing the result of the previous multiplication by the "general" probability of the data (P(D)). So at this level the only thing we need is one multiplication and one division. However, it turns out that P(D) is very hard, i.e., practically impossible to calculate so we cannot calculate the probability of the model after all. Luckily, the Bayes rules still helps us to do something meaningful.

Comparing the probabilities of two models

Even if one cannot compute the probability of the dependency model exactly (since we cannot compute P(D)), Bayes rule makes it possible for us to calculate what is the ratio of the probabilities of two models. This way we can answer the questions like "if we have the data D, is the dependency model M1 more probable than dependency model M2 and if so, how many times more probable ?"

Some formulas again. Let us denote data with D as previously and let us now have two different dependency models M1 and M2. Now the ratio of probabilities P(M1 | D) / P(M2 | D) can be calculated using the Bayes rule:

P(M1 | D) / P(M2 | D) = [P(D | M1) * P(M1) / P(D)] / [P(D | M2) * P(M2) / P(D)],

and since P(D) appears in both formulas in the same position it cancels out so that

P(M1 | D) / P(M2 | D) = [P(D | M1) * P(M1)] / [P(D | M2) * P(M2) ].

This way we can compare the probabilities of the models without calculating the difficult part P(D). Since probabilities are never negative, ratio P(M1 | D) / P(M2 | D) being greater than one can only happen if M1 is more probable than M2 (i.e. P(M1 | D) > P(M2 | D)). Similarly the only explanation for ratio to be less than 1 is that M1 is less probable than M2.

It is also easy to understand that since we can compare the probabilities of any two models, we can say which model is the most probable in any finite set of models. The brute force way of doing this is to first compare any two models, pick the more probable one and compare that with third model, again pick the "winner" of the latest comparison and compare it with the fourth model and so on. The model that wins the last comparison is the most probable one.

So this is all fine in theory, as long as we can really calculate the probabilities P(D | M) and P(M). Let as start with the easier one.

How can we calculate P(M)?

There is actually nothing to calculate. P(M), the probability of model M before we have seen any data, is what is called prior probability (that is just a fancy name for probabilities that have to be determined before seeing data). Bayesians try to determine this subjective probability by using their background knowledge. A common way to determine prior probabilities for data analysis purposes is to try to let the data "speak" and not to favor any models beforehand. That is why in B-Course we think that all the models are equally probable before we have seen any data. This means that P(M1) = P(M2) for any two models M1 and M2.

This also means that comparison of models is further simplified since now P(M1) and P(M2) cancel out and we get:

P(M1 | D) / P(M2 | D) = P(D | M1) * P(M1)] / [P(D | M2) * P(M2) ] = P(D | M1) / P(D | M2)

This leaves us just with the calculation of P(D | M).

How can we calculate P(D | M)?

All the previous terms we have got rid of without calculating them. However, it is evident that something has to be calculated and P(D | M) is just that part. The story how this thing can be calculated for discrete data is long and it can be found in the reference below, but to tell how it ends is somewhat easy. It can be shown that there is a formula with which we can calculate P(D | M). That formula has many multiplications and functions called gamma functions:

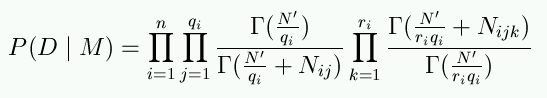
The formula is complicated, and we are not even trying to explain it in detail, but it is still nice to know what those different letters in the formula mean so that one can get an idea what this calculation is based on - after all we are calculating P(D | M) so there cannot be much more than those things that are in our model M or our data D. Before sorting out the notations, the columns in the beginning mean multiplication and the funny hook is called gamma function.

• n is number of variables, i indexes variables from 1 to n.
• r_i is number of values in i:th variable. k indexes these values from 1 to r_i (so we can say k:th value of i:th variable).
• q_i is the number of possible configurations of parents of i:th variable. Parents of i:th variable are those variables from which there is an arc to i:th variable in our model. With number of configurations of the parents we mean the number of different value combinations parent variables can take. q_i can actually be calculated by multiplying the number of values each parent variable has. We have enumerated these value combinations and index them with j that goes from first value combination to q_ith value combination.
• N_ij tells how many rows in a data have j:th configuration for parents of i:th variable.
• N_ijk tells how many rows in data that have k:th value for the i:th variable also have j:th configuration for parents of i:th variable.
• The only thing left to mention is N', the equivalent sample size. It is a parameter that determines how easily we change our beliefs about the quantitative nature of dependencies when we see data. If N' is big, we do not believe data very easily, if it is small we believe every quirk of it. What would be the suitable N' for a rational Bayesian agent? This question is not easy to answer. B-Course makes a simple choice that is remotely inspired by so called Jeffreys prior. N' is set to be the average number of values variables have (after discretization) divided by two. Different ways to choose N' lead to different probabilities of the models (!). This means that if we choose the N' differently, we may well have different result, when we try to find the most probable model.

» References to calculating P(D | M)
» References to Jeffreys prior

B-Course, version 2.0.0	CoSCo 2002