| home | library | feedback |
Inferring causality from statistical dependence is debatable as it should be. However, causal models have many desirable properties, so the task is worth pursuing. It also appears that by making some additional assumptions, inferring causalities from observed statistical dependencies can be justified. Unfortunately, we are not aware of any simple way of explaining this.
» References to more detailed explanations
of inferring causation in naive model
Arguing that we can infer causality from statistical dependencies necessarily relies on the properties of causality and statistical dependencies. While people seem to be naturally good in inferring about causality they are not naturally talented in making inferences about statistical dependencies. So we need to take a difficult road and call formalisms and logic for help. The prerequisite for accurately following the arguments below is that you can read the dependencies from Bayesian network. If you cannot, you are still encouraged to read the explanation to get the general idea of what sort of reasoning the inferred causality is built on.
In general it is somewhat plausible to think that all the dependencies between things in the world are due to some kind of causal mechanism. In naive model we make an additional assumption that all the dependencies between variables are due to the causal relationships between variables in the model. So in effect we deny the possibility that we have excluded some variables that could cause dependencies in our model. That equals saying that we deny the possibility of latent causes. Now you probably see why this model is called naive.
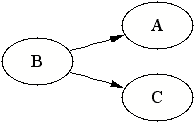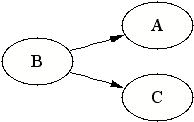
If we, however, make the naive assumption of excluding latent variables the inference of causes seem to become possible since all the unconditional dependencies between A and B (A and B are dependent of each other no matter what we know or don't know about other variables) must be explained by either A causing B or B causing A. But how can we know the direction of causality? We cannot always, but sometimes we are lucky to have such a model, that the coexistence of dependencies cannot be explained without a certain causal relationship. If A and B seem to be dependent no matter what and B and C seem to be dependent no matter what, but A and C are not dependent of each other if we know something about certain other variables S (S can be empty), and nothing about B and the rest of the variables, then we know for sure that A has causal effect on B. How come? This is because B cannot be the cause of A or otherwise A and C would always be dependent too, but we just said that that sometimes (given S not containing B) they are independent.
Now let us be a little bit more rigorous, so that this becomes almost a proof now. So let us assume that our model contains following dependence statements:
Clearly A cannot be a direct cause of C since if A were a direct cause of C then A and C would always be dependent and that is against the dependence statement 3 in our model. For the very same reason C cannot be a direct cause of A. So we are left with following four possibilities (NB. The arcs denote causalities):
| In this case A and C would always appear dependent as long as we do not know B (so A and B would be dependent given S), since unknown common cause makes the effects look dependent. But by dependency statement 3, A and C cannot be always dependent, so this possibility is ruled out. |  |
| In this case A and C would always be dependent given S, since S does not contain B and knowing something about B is the only way to block the dependency from A to C (via B). |  |
| In this case A and C would always be dependent given S, since S does not contain B and knowing something about B is the only way to block the dependency from C to A (via B). |  |
| Since B is a collision node, it blocks the dependency flow from A to C. This is the only model that is consistent with all the three dependency statements of our model above. | 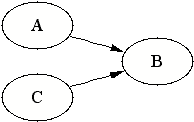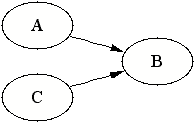 |
| B-Course, version 2.0.0 | |