What do we do with the missing data

Missing data is a problem for many statistical procedures, B-Course is not an exception. Bayesian theory has a very clear philosophical answer to the lack of information caused by missing data. Unfortunately, this answer is computationally infeasible, so we end up doing something much simpler, and not so well theoretically justified.

We do not count missing data

The most simple way to handle missing data is to throw away all the data rows that have some missing entries. The other possibility is to impute the missing data. That means guessing some values to those entries of the data matrix that are missing. After imputation we could then continue the analysis as if there were no missing data at all. B-Course does something between these two extremes. It tries to throw away only those parts of the data row that are missing. In fact for technical reasons B-Course discards a little bit more than this. The explanation below is somewhat technical, but we encourage you to read it anyway, so you can get an idea of what kind of approach B-Course is using and what are the problematic parts of this approach to missing data handling.

To understand the way B-Course handles missing data we have to look at our goal. We are trying to find a probable dependency model. To do so we have to be able to compare the probabilities of different models. This comparison is essentially based on our ability to calculate the probability of data D based on our model M. This all is explained in our library text on calculating the probability of a dependency model. The calculation of P(D|M) is made using a slightly complicated looking formula below.

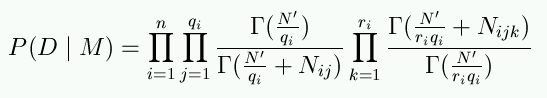
Rather than trying to explain the formula for P(D|M), we just make couple of observations about it. It seems to be based partly on the things that are marked N_ij and N_ijk. These things are actually frequencies that tell us on how many rows in our data we can find a certain combination of values. Hence they are simple counters of certain value combinations in the data. When a data row has missing values, we do not know which value combinations it had if the data were not missing. If, due to some missing data, we do not know if certain value combination occurs on a row or not, we do not count it as occurring, i.e., we do not increase the corresponding N_ijk by one. This way we end up with smaller N_ijks than if there were no missing data. So far everything is OK, we just do not count certain value combinations, because we cannot know if they occur, since the data is missing. But here comes the problematic part: we still use the formula above, now with our N_ijks (and N_ijs) that have been calculated from the missing data. Strictly speaking, the formula above is only valid for the data sets that have no missing data.

For those of you who find not appropriate the current way B-Course takes to handle missing data, we can give couple of alternatives that you as a user can adopt.

Suggestion 1: Mark missing values with "?"

Often values are not missing completely at random. Since B-Course will deal with discrete values anyway, it is often a good idea to handle missing values as a legitimate values for a variable. This should be done anyway, if we suspect that there is some systematic reason for values to be missing. Of course, handling missing values as "ordinary" values is not meaningful, if the amount of missing values is very small (like once in a one variable). To treat missing data as value of its own you can simply replace missing positions with any name you like (like ?, missing, *, no answer, etc) as long as your newly created value name does not clash with existing values.

Suggestion 2: Impute manually

You are of course always free to impute missing data before you upload it into the B-Course.

B-Course, version 2.0.0	CoSCo 2002